
What is forex market?
The foreign exchange market is where currencies are traded. Currencies are important because they allow us to purchase goods and services locally and across borders. International currencies need to be exchanged to conduct foreign trade and business.
If you are living in the United States and want to buy cheese from France, then either you or the company from which you buy the cheese has to pay the French for the cheese in euros (EUR). This means that the U.S. importer would have to exchange the equivalent value of U.S. dollars (USD) for euros.
Forex (FX) is a portmanteau of foreign currency and exchange. Foreign exchange is the process of changing one currency into another for a variety of reasons, usually for commerce, trading, or tourism. According to a 2019 triennial report from the Bank for International Settlements (a global bank for national central banks), the daily trading volume for forex reached $6.6 trillion in 2019.
The foreign exchange (also known as forex or FX) market is a global marketplace for exchanging national currencies. Currencies trade against each other as exchange rate pairs. For example, EUR/USD is a currency pair for trading the euro against the U.S. dollar.
The goal of an algorithmic trader is to develop a program that ultimately helps us make better trading decisions.

In this project we will do the following:
Connecting to mt5 Platform
We will use the script below is to connect to a trading account using specified parameters
import MetaTrader5 as mt5# display data on the MetaTrader 5 package print("MetaTrader5 package author: ",mt5.__author__) print("MetaTrader5 package version: ",mt5.__version__) # establish connection to the MetaTrader 5 terminal if not mt5.initialize(): print("initialize() failed, error code =",mt5.last_error()) quit() # display data on MetaTrader 5 version print(mt5.version()) # now connect to another trading account specifying the password account=58548216 authorized=mt5.login(account, password="h1gcnplo", server="AdmiralMarkets-Demo") if authorized: # display trading account data 'as is' print(mt5.account_info()) # display trading account data in the form of a list print("Show account_info()._asdict():") account_info_dict = mt5.account_info()._asdict() for prop in account_info_dict: print(" {}={}".format(prop, account_info_dict[prop])) else: print("failed to connect at account #{}, error code: {}".format(account, mt5.last_error()))
Collecting data
Get data from the MetaTrader 5 terminal starting from the specified index.
Let we choose a timeframe equal to 1 hour and retrieve data starting from 10000 bars from the past till now.
rates = mt5.copy_rates_from_pos("EURUSD", mt5.TIMEFRAME_H1, 0, 10000)
rates_frame = pd.DataFrame(rates)That is a sample of 10 rows in our dataset.
rates_frame.sample(10)
Open: Opening price
Hight: Highest price
Low: Lowest pice
Close: Closing price
Our target is to predict the closing price so we have to create a new variables.
Creating new features
I. Simple moving average
A simple moving average (SMA) is an arithmetic moving average calculated by adding recent prices per exemple (closing price or openning price) and then dividing that figure by the number of time periods in the calculation average.
For example, one could add the closing price of a security for a number of time periods and then divide this total by that same number of periods.
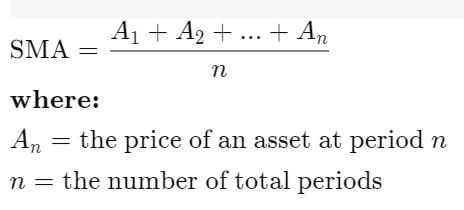
A simple moving average is customizable because it can be calculated for different numbers of time periods.
def SMA(data, period, price):
# adding NaN value by default at the beginning.
SMA_list = [np.nan for j in range(period-1)]
for i in range(0, len(data)-period+1):
x = round(float(data[[price]].loc[i:i+period-1].sum())/period, 5)
SMA_list.append(x)
return SMA_listLet we choose n equal to 10 periods and we fix An to the openning price of an asset.
rates_frame['SMA'] = SMA(data=rates_frame, period=10, price='open')
rates_frame.sample(5)
II. Exponentiel Simple moving average
An exponential moving average (EMA) is a type of moving average (MA) that places a greater weight and significance on the most recent data points.The exponential moving average is also referred to as the exponentially weighted moving average.
An exponentially weighted moving average reacts more significantly to recent price changes than a simple moving average simple moving average (SMA), which applies an equal weight to all observations in the period.
EMA = Opening price * multiplier + EMA (previous day) * (1-multiplier)
Where
multiplier = [2 / (number of observations + 1)]
def EMA(data, period, price):
# the first values of EMA are a NAN values
EMA_list = [np.nan for i in range(period-1)]
# the first value of EMA (not a NAN value) equal to the first value (not a NAN value) of SMA
EMA_list.append(SMA(rates_frame, period, price)[period -1])
multiplier = 2 / (period + 1)
for i in range(period, len(data)):
EMA_value = round(float(data[[price]].loc[i])*multiplier + EMA_list[i-1]*(1-multiplier), 5)
EMA_list.append(EMA_value)
return EMA_list
rates_frame['EMA'] = EMA(data=rates_frame, period=10, price='open')
rates_frame.tail(5)
III. Triple exponential moving average
The triple exponential moving average (TEMA) was designed to smooth price fluctuations, thereby making it easier to identify trends without the lag associated with traditional moving averages (MA).
It does this by taking multiple exponential moving averages (EMA) of the original EMA and subtracting out some of the lag.
Triple Exponential Moving Average (TEMA) = 3*EMA1 - 3*EMA2 + EMA3
Where:
EMA1 = Exponential moving average of EMA
EMA2 = EMA of EMA1
EMA3 = EMA of EMA2
rates_frame['EMA1'] = EMA1(data=rates_frame, period=10, price='EMA')
rates_frame['EMA2'] = EMA2(data=rates_frame, period=10, price='EMA1')
rates_frame['EMA3'] = EMA3(data=rates_frame, period=10, price='EMA2')
rates_frame['TEMA'] = 3*rates_frame['EMA1'] - 3*rates_frame['EMA2'] + rates_frame['EMA3']
rates_frame = rates_frame.drop(['EMA1', 'EMA2', 'EMA3'], axis=1)IV. Moving Average Convergence/Divergence MACD
MACD is calculated by subtracting the long-term EMA (26 periods) from the short-term EMA (12 periods). An EMA is a type of moving average (MA) that places a greater weight and significance on the most recent data points.
MACD = 12-Period EMA − 26-Period EMA
rates_frame['MACD'] = np.array(EMA(data=rates_frame, period=12, price='open')) - np.array(EMA(data=rates_frame, period=26, price='open'))Analytical Study
Our goals in this part is:
- Find out useful information by looking at different data points and their availability and distribution in the given dataset.
- Finding out how different variables correlate to each other based on their availability.
I. Graph visualization
import matplotlib.pyplot as plt
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(12, 8))
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=18,
titlepad=10,
)
plot_params = dict(
color="0.75",
style=".-",
markeredgecolor="0.25",
markerfacecolor="0.25",
legend=False,
)
%config InlineBackend.figure_format = 'retina'
ax = rates_frame['close'][400:700].plot(**plot_params)
ax = rates_frame['close'][400:700].plot(ax=ax, linewidth=3, legend=True)
ax.set_title('Time Plot of Tunnel Traffic');
rates_frame['SMA'][400:700].plot(ax=ax, linewidth=3, title="Tunnel Traffic - Simple Moving Average", legend=True);
rates_frame['EMA'][400:700].plot(ax=ax, linewidth=3, title="Tunnel Traffic - Simple Moving Average", legend=True);
rates_frame['TEMA'][400:700].plot(ax=ax, linewidth=3, title="Tunnel Traffic - Moving Average", legend=True);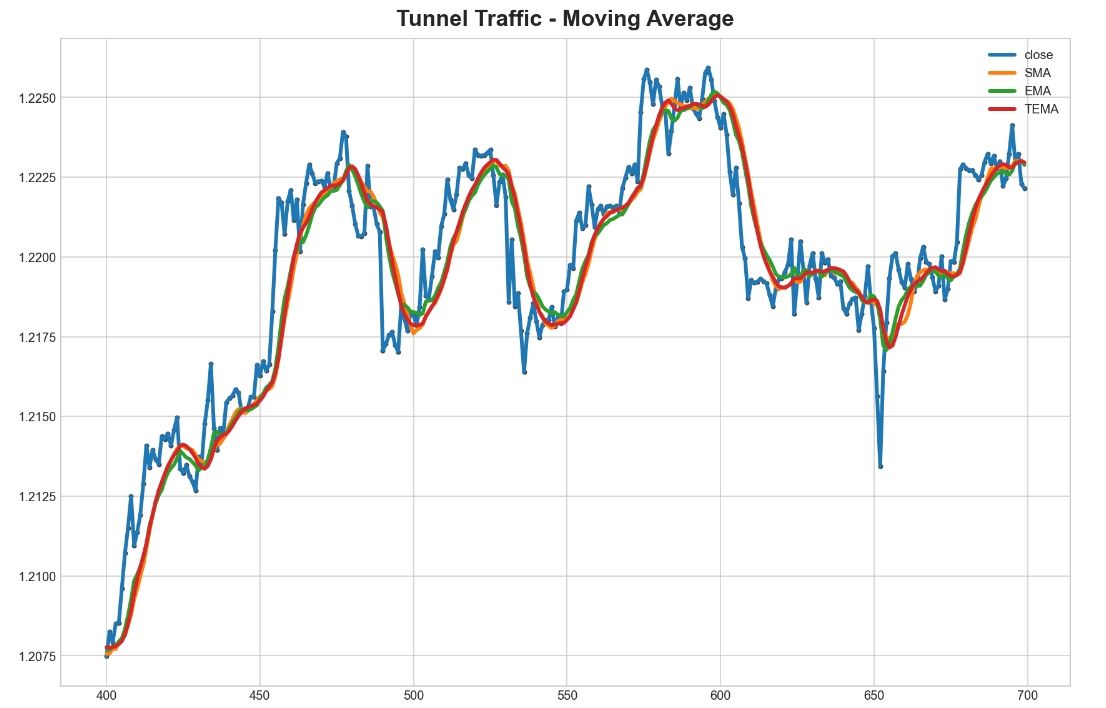
II. Correlation relation between features
Let us discover the correlation strength between all features using the Heatmap.
import seaborn as sns
corr = rates_frame[['SMA', 'EMA', 'MACD', 'TEMA', 'close']].corr()
# Set up the matplotlib plot configuration
f, ax = plt.subplots(figsize=(12, 5))
# Generate a mask for upper traingle
mask = np.triu(np.ones_like(corr, dtype=bool))
# Configure a custom diverging colormap
cmap = sns.diverging_palette(230, 20, as_cmap=True)
# Draw the heatmap
sns.heatmap(corr, annot=True, mask = mask, cmap=cmap)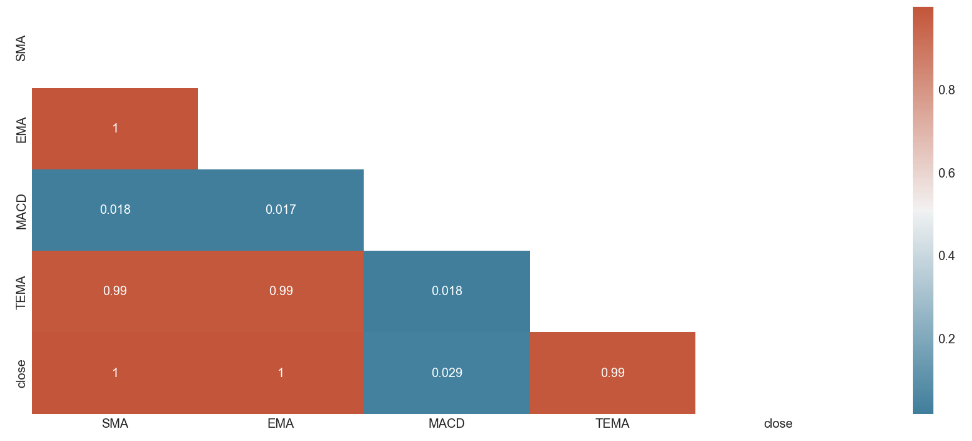
From the above correlation heatmap, one could get some of the following information:
- Variables SMA, EMA, TEMA are having strong positive correlation with the closing price. Generally speaking, a Pearson correlation coefficient value greater than 0.7 indicates the presence of multi-collinearity.
- The variable MACD have no correlation with the closing price.
III. descriptive statistics
let we show the central tendency, shape, distribution, and dispersion of variables.
rates_frame[['close', 'TEMA', 'MACD', 'EMA', 'SMA']].describe().transpose()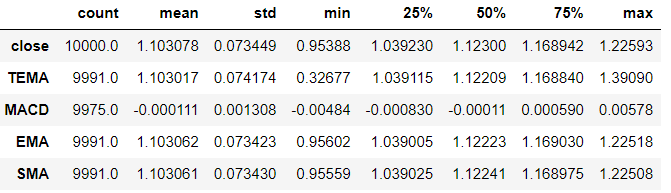
Modelling
In this part we will try to predict the closing price of EUR/USD
I. Data normalization
The goal of normalization is to change the values of numeric columns in the dataset to a common scale, without distorting differences in the ranges of values.
from sklearn.preprocessing import StandardScaler
data = df[['SMA', 'EMA', 'TEMA']]
scaler = StandardScaler()
data = pd.DataFrame(scaler.fit_transform(data), columns=data.columns)II. Model
We will use a simple sequential model with one layer and we fix the optimizer to 'sgd' and the loss function to 'MSE'.

from tensorflow.keras import Sequential, layers
model = Sequential([layers.Dense(units=1, input_shape=[3])])
model.compile(optimizer='sgd', loss='MSE')
model.summary()We will train the model by repeatedly iterating over the data between 7999 and 9000 observations of our dataset for 1000 epochs.
history = model.fit(data[['SMA', 'EMA', 'TEMA']][8000:9000], df['close'][8000:9000], epochs=100, validation_split = 0.2)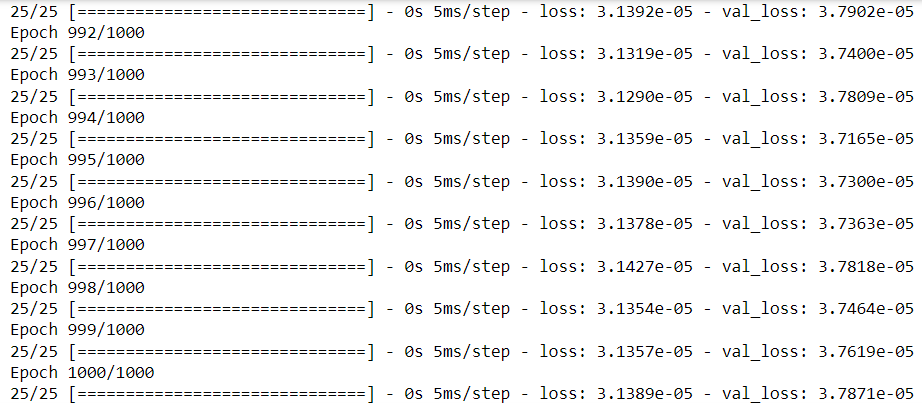
We evaluate the model on the last observations
score = model.evaluate(data[['SMA', 'EMA', 'TEMA']][9000:], df['close'][9000:])
print(score)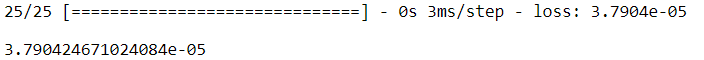
III. Model visualization
import matplotlib.pyplot as plt
def plot_loss(history):
plt.figure(figsize=(12, 5))
plt.plot(history.history['loss'][100:], label='loss')
plt.plot(history.history['val_loss'][100:], label='val_loss')
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
From the plot of the loss function, you can see that the model has a high performance.
Summary
In this project, you discovered the importance of creating a new features and reviewing metrics while training your deep learning models.